tea加密算法

一，简介

tea 的全称为”Tiny Encryption Algorithm”，是由剑桥大学计算机实验室的 David Wheeler 和 Roger Needham于1994年发明的加密算法。特点是加密解密速度快，实现简单。

tea 算法明文分组为 64bit(8byte)，采用 128bit(16byte) 作为 key，算法采用迭代的形式，推荐的迭代轮数是 64轮，最少 32 轮。

二，算法原理

流程如下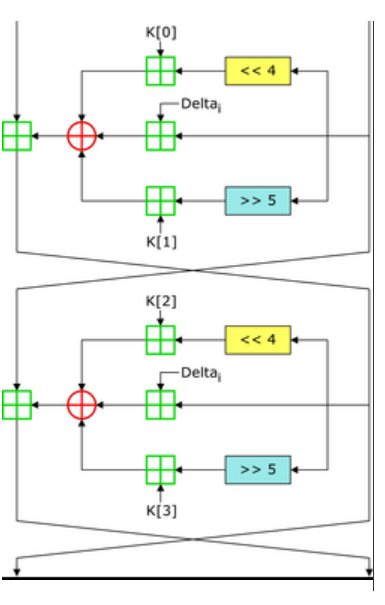

1，初始化：

将明文分成两个32位的块（通常是64位的明文分成两个32位的部分

将128位的密钥分成四个32位的子密钥

2，加密轮数

通常进行32轮加密，每轮使用一个常量DELTA来确保子密钥的独特性

3，每轮加密操作：

在每一轮中，使用以下公式对两个32位的块进行操作：

​ v0=(v0+((v1<<4)+k0)⊕(v1+sum)⊕((v1>>5)+k1)) mod 232

​ v1=(v1+((v0<<4)+k2)⊕(v0+sum)⊕((v0>>5)+k3)) mod 232

其中，v0 和 v1是两个32位的块，k0、k1、k2、k3是子密钥，sum是一个累加的常量，每轮增加 DELTA

三，代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
from Crypto.Util.number import bytes_to_long, long_to_bytes

DELTA = 0x9e3779b9
NUM_ROUNDS = 32

def encrypt(plain_text, key):
    """
    参数:
    plain_text: 明文字节串。
    key: 加密密钥 长度为16字节。

    返回:
    加密后的密文字节串。
    """
    v0 = bytes_to_long(plain_text[:4])
    v1 = bytes_to_long(plain_text[4:])
    k = [bytes_to_long(key[i:i+4]) for i in range(0, 16, 4)]
    sum = 0
    for _ in range(NUM_ROUNDS):
        sum = (sum + DELTA) & 0xffffffff
        v0 = (v0 + (((v1 << 4) + k[0]) ^ (v1 + sum) ^ ((v1 >> 5) + k[1]))) & 0xffffffff
        v1 = (v1 + (((v0 << 4) + k[2]) ^ (v0 + sum) ^ ((v0 >> 5) + k[3]))) & 0xffffffff
    # 将加密后的v0和v1转换为字节串并返回
    return long_to_bytes(v0, 4) + long_to_bytes(v1, 4)

def decrypt(cipher_text, key):
    """
    参数:
    cipher_text: 密文字节串。
    key: 解密密钥 长度为16字节。

    返回:
    解密后的明文字节串。
    """
    v0 = bytes_to_long(cipher_text[:4])
    v1 = bytes_to_long(cipher_text[4:])
    k = [bytes_to_long(key[i:i+4]) for i in range(0, 16, 4)]
    sum = (DELTA * NUM_ROUNDS) & 0xffffffff
    # 迭代执行32轮解密操作
    for _ in range(NUM_ROUNDS):
        v1 = (v1 - (((v0 << 4) + k[2]) ^ (v0 + sum) ^ ((v0 >> 5) + k[3]))) & 0xffffffff
        v0 = (v0 - (((v1 << 4) + k[0]) ^ (v1 + sum) ^ ((v1 >> 5) + k[1]))) & 0xffffffff
        sum = (sum - DELTA) & 0xffffffff
    # 将解密后的v0和v1转换为字节串并返回
    return long_to_bytes(v0, 4) + long_to_bytes(v1, 4)

# 示例用法
key = b'0123456789abcdef'  # 16字节密钥
plain_text = b'hello123'  # 8字节明文

cipher_text = encrypt(plain_text, key)
print(f'加密后的密文: {cipher_text}')

decrypted_text = decrypt(cipher_text, key)
print(f'解密后的明文: {decrypted_text}')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
using namespace std;

void Encrypt(long* EntryData, long* Key) {
    //分别加密数组中的前四个字节与后4个字节,4个字节为一组每次加密两组
    unsigned long x = EntryData[0];
    unsigned long y = EntryData[1];

    unsigned long sum = 0;
    unsigned long delta = 0x9E3779B9;
    //总共加密32轮
    for (int i = 0; i < 32; i++) {
        sum += delta;
        x += ((y << 4) + Key[0]) ^ (y + sum) ^ ((y >> 5) + Key[1]);
        y += ((x << 4) + Key[2]) ^ (x + sum) ^ ((x >> 5) + Key[3]);
    }
    //最后加密的结果重新写入到数组中
    EntryData[0] = x;
    EntryData[1] = y;
}

void Decrypt(long* EntryData, long* Key) {
    //分别加密数组中的前四个字节与后4个字节,4个字节为一组每次加密两组
    unsigned long x = EntryData[0];
    unsigned long y = EntryData[1];

    unsigned long sum = 0;
    unsigned long delta = 0x9E3779B9;
    sum = delta << 5;   //注意这里,sum = 32轮之后的黄金分割值. 因为我们要反序解密.
    //总共加密32轮 那么反序也解密32轮
    for (int i = 0; i < 32; i++) {
        // 先将y解开 然后参与运算在解x
        y -= ((x << 4) + Key[2]) ^ (x + sum) ^ ((x >> 5) + Key[3]);
        x -= ((y << 4) + Key[0]) ^ (y + sum) ^ ((y >> 5) + Key[1]);
        sum -= delta;
    }
    //最后加密的结果重新写入到数组中
    EntryData[0] = x;
    EntryData[1] = y;
}

int main() {
    long Data[3] = {1, 2};  //明文，必须是8字节的倍数，不够需要程序补全，参考base64方法
    printf("待加密的数值：%d %d\n",Data[0],Data[1]);  

    long key[4] = {2,2,3,4 };   //密钥随便

    //Encrypt每次只是加密4字节数组中的两组(也就是每次加密8个字节) 如果你数据多.可以来个for循环来循环加密,但是Entrypt内部还有32次循环,所以速度上还是会有点影响.
    Encrypt(Data, key);
    printf("加密后的数值：%d %d\n",Data[0],Data[1]);
    Decrypt(Data, key);
    printf("解密后的数值：%d %d\",Data[0],Data[1]);
    system("pause");
}