没e也能玩

直接了当的dp,dq泄露攻击，不需要e

1
2
3
4
5
6
7
8
9
10
p = getPrime(1024)
q = getPrime(1024)
d = inverse(65537,(p-1)*(q-1))
dp = d %(p-1)
dq = d%(q-1)
print(f'c={pow(bytes_to_long(flag),e,p*q)}')
print(f'p={p}')
print(f'q={q}')
print(f'dp={dp}')
print(f'dq={dq}')

直接流程解密即可

1
2
3
4
5
6
7
8
9
10
c=
p=
q=
dp=
dq=
InvQ=gmpy2.invert(q,p)
mp=pow(c,dp,p)
mq=pow(c,dq,q)
m=(((mp-mq)*InvQ)%p)*q+mq
print(long_to_bytes(m))

flag{No_course_e_can_play}

格格你好棒

根据题目提示，可知应该是造个格就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
flag = b'******'
m = bytes_to_long(flag)
a = getPrime(1024)
b = getPrime(1536)
p = getPrime(512)
q = getPrime(512)
r = random.randint(2**14, 2**15)
assert ((p+2*r) * 3*a + q) % b < 70

c = pow(m, 0x10001, p*q)

print(f'c =', c)
print(f'a =', a)
print(f'b =', b)

不等式的右边只有70，爆破即可 根据等式造格

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from Crypto.Util.number import *

e=0x10001
c = 
a = 
b = 
M = matrix(ZZ, [
  [1, 3*a],
  [0,   b]
])
L = M.LLL()
p_2r,q_t= L[0]
p_2r=abs(p_2r)
q_t=abs(q_t)

print(p_2r,q_t)

for i in range(70):
    p=q_t+i
    d=inverse(e,p-1)
    if b'flag' in long_to_bytes(int(pow(c,d,p))):
        print(long_to_bytes(int(pow(c,d,p))))

flag{u_are@master_of_latt1ce_Crypt0gr@phy}

easy_ecc

基础的ecc，参数都全，没什么玄机

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
p = 
a = 
b = 
E = EllipticCurve(GF(p),[a,b])
m = E.random_point()
G = E.random_point()
k = 
K = k * G
r = getPrime(256)
c1 = m + r * K
c2 = r * G
c_left =bytes_to_long(flag[:len(flag)//2]) * m[0]
c_right = bytes_to_long(flag[len(flag)//2:]) * m[1]

print(f"c1 = {c1}")
print(f"c2 = {c2}")
print(f"cipher_left = {c_left}")
print(f"cipher_right = {c_right}")

求得m之后c1，c2除掉相应量即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from Crypto.Util.number import *
p = 
a = 
b = 
k = 
E = EllipticCurve(GF(p),[a,b])
c1 = E(,)
c2 = E(,)
c_left = 
c_right = 

m=c1-k*c2
m1=int(c_left//m[0])
m2=int(c_right//m[1])
print(long_to_bytes(m1)+long_to_bytes(m2))

flag{This_is_the_last_crypto_}

RSA？cmd5！

简单的签名过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
# 什么 你说你用md5给rsa签名了 

m = '*******'
assert len(m) == 7
flag = 'flag{th1s_1s_my_k3y:' + m + '0x' + hashlib.sha256(m.encode()).hexdigest() + '}'

p = getStrongPrime(512)
q = getStrongPrime(512)
n = p * q
e = 65537
phi = (p - 1) * (q - 1)
d = inverse(e, phi)


def get_MD5(m0):
    import hashlib
    md5_object = hashlib.md5(m0.encode())
    md5_result = md5_object.hexdigest()
    return md5_result


def get_s(m0, d0, n0):
    hm0 = get_MD5(m0)
    hm1 = bytes_to_long(hm0.encode())
    s0 = pow(hm1, d0, n0)
    return s0


def rsa_encode(m0, e0, n0):
    m1 = bytes_to_long(m0.encode())
    c0 = pow(m1, e0, n0)
    return c0


def get_flag(m0):  # 请用这个函数来转m得到flag
    import hashlib
    flag = 'flag{th1s_1s_my_k3y:' + m0 + '0x' + hashlib.sha256(m0.encode()).hexdigest() + '}'
    print(flag)


s = get_s(m, d, n)
c = rsa_encode(flag, e, n)

print("密文c =", c)
print("签名s =", s)
print("公钥[n,e] =", [n, e])

根据题目提示，cmd5解一下得到了m='adm0n12'

1
2
3
4
5
6
7
8
9
10
11
12
13
def get_flag(m0):  # 请用这个函数来转m得到flag
    import hashlib
    flag = 'flag{th1s_1s_my_k3y:' + m0 + '0x' + hashlib.sha256(m0.encode()).hexdigest() + '}'
    print(flag)
    
c = 
s = 
n,e = [, 65537]
hm=pow(s,e,n)
print(long_to_bytes(hm))

m='adm0n12'
flag=get_flag(m)

b’86133884de98baada58a8c4de66e15b8’ flag{th1s_1s_my_k3y:adm0n120xbfab06114aa460b85135659e359fe443f9d91950ca95cbb2cbd6f88453e2b08b}

故事新编1

使用网站解密 Vigenere Solver | guballa.de

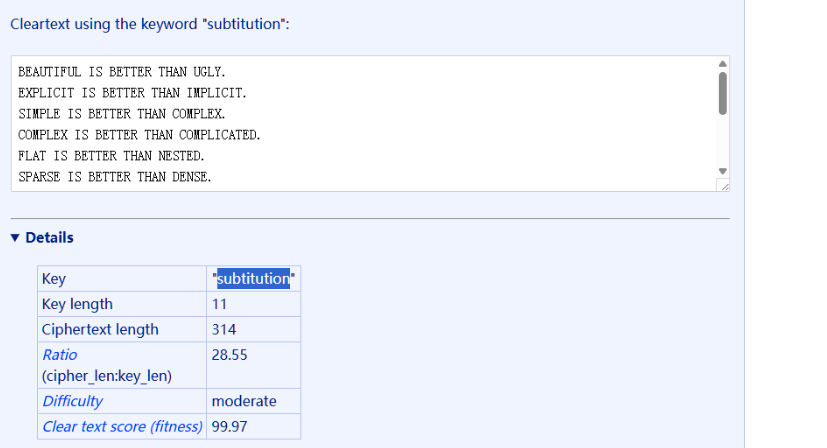
密钥为：subtitution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from hashlib import md5

words='''
BEAUTIFUL IS BETTER THAN UGLY.
EXPLICIT IS BETTER THAN IMPLICIT.
SIMPLE IS BETTER THAN COMPLEX.
COMPLEX IS BETTER THAN COMPLICATED.
FLAT IS BETTER THAN NESTED.
SPARSE IS BETTER THAN DENSE.
FLAGA IS VEGENERE
READABILITY COUNTS.
SPECIAL CASES AREN'T SPECIAL ENOUGH TO BREAK THE RULES.
ALTHOUGH PRACTICALITY BEATS PURITY.
ERRORS SHOULD NEVER PASS SILENTLY.
UNLESS EXPLICITLY SILENCED.

'''
flag = b'flag{'+md5(words.encode()).hexdigest().encode()+b'}'
print(flag)

`flag{bda2bcf1eaeff7754a6483e74e70a937}

故事新编2

继续使用网站解密，模式改为AutoKey模式即可

密钥为：supersubtitution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from hashlib import md5
words='''
IN THE FACE OF AMBIGUITY, REFUSE THE TEMPTATION TO GUESS.
THERE SHOULD BE ONE-- AND PREFERABLY ONLY ONE --OBVIOUS WAY TO DO IT.
ALTHOUGH THAT WAY MAY NOT BE OBVIOUS AT FIRST UNLESS YOU'RE DUTCH.
NOW IS BETTER THAN NEVER.
ALTHOUGH NEVER IS OFTEN BETTER THAN RIGHT NOW.
IF THE IMPLEMENTATION IS HARD TO EXPLAIN, IT'S A BAD IDEA.
IF THE IMPLEMENTATION IS EASY TO EXPLAIN, IT MAY BE A GOOD IDEA.

'''

flag = b'flag{'+md5(words.encode()).hexdigest().encode()+b'}'
print(flag)

flag{8bc383165248f2e45a6910960a61e6a8}

不用谢喵

查看题目发现encrypto是iv+enc，刚好是iv加两组CBC模式加密结果

给出decrypto为ECB模式下对encrypto的解密结果。

根据CBC模式的特点

将密文分为两组，enc1和enc2。两组ECB模式解密后分别是 异或回去即可

1
2
3
4
5
6
enc="f2040fe3063a5b6c65f66e1d2bf47b4cddb206e4ddcf7524932d25e92d57d3468398730b59df851cbac6d65073f9e138"
dec="f9899749fec184d81afecd35da430bc394686e847d72141b3a955a4f6e920e7d91cb599d92ba2a6ba51860bb5b32f23b"

a=int(dec[32:64],16)^int(enc[:32],16)
b=int(dec[64:],16)^int(enc[32:64],16)
print(long_to_bytes(a).decode(),long_to_bytes(b).decode())

flag{HOw_c4REfu1 Ly_yOu_O65ERve!}

没e这能玩？

解方程得到p,q,r。

离散对数得到e，解密即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
pqr= [ ..., ... , ...] 
big_prime = ...
hint= ...   
c = ...
p,q,r=symbols('p,q,r')
h1 = 1*p + 1*q + 1*r
h2 = 2*p + 3*q + 3*r
h3 = 9*p + 9*q + 6*r
roots=solve([h1-pqr[0],h2-pqr[1],h3-pqr[2]],[p,q,r])
p,q,r=int(roots[p]),int(roots[q]),int(roots[r])
"""
#sage
n=2^512
big_prime= 10340528340717085562564282159472606844701680435801531596688324657589080212070472855731542530063656135954245247693866580524183340161718349111409099098622379
hint=      1117823254118009923270987314972815939020676918543320218102525712576467969401820234222225849595448982263008967497960941694470967789623418862506421153355571 
mod=Zmod(n)
e=discrete_log(mod(hint),mod(big_prime))
e
"""
e=18344052974846453963
d=inverse(e,(p-1)*(q-1)*(r-1))
print(long_to_bytes(pow(c,d,p*q*r)))

flag{th1s_2s_A_rea119_f34ggg}

两个黄鹂鸣翠柳

两个明文见存在线性关系，使用Franklin-Reiter-相关信息攻击即可，

大致原理在这篇文章中 相关信息攻击-Franklin-Reiter-CSDN博客

将其中爆破e的部分改为爆破t1，t2即可，大概20分钟左右解出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from Crypto.Util.number import *
from tqdm import tqdm 
e =  683
c1 = ...
c2 = ...
n = ...
delta = ...

def franklinReiter(n,e,c1,c2,t1,t2):
    PR.<x> = PolynomialRing(Zmod(n))
    g1 = (x+t1)^e - c1
    g2 = (x+t2)^e - c2

    def gcd(g1, g2):
        while g2:
            g1, g2 = g2, g1 % g2
        return g1.monic()
    return -gcd(g1, g2)[0]

for t1 in tqdm(range(255,1,-1)):
    for t2 in tqdm(range(255,1,-1)):
        m=franklinReiter(n,e,c1,c2,t1*delta%n,t2*delta%n)
        flag = long_to_bytes(int(m))
        if b'{' in flag and b'}' in flag:
            print(flag)

这是几次方？ 疑惑！

不知道为啥逆回去不对，把爆破一下得了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
c = 36513006092776816463005807690891878445084897511693065366878424579653926750135820835708001956534802873403195178517427725389634058598049226914694122804888321427912070308432512908833529417531492965615348806470164107231108504308584954154513331333004804817854315094324454847081460199485733298227480134551273155762
n, e = [124455847177872829086850368685666872009698526875425204001499218854100257535484730033567552600005229013042351828575037023159889870271253559515001300645102569745482135768148755333759957370341658601268473878114399708702841974488367343570414404038862892863275173656133199924484523427712604601606674219929087411261, 65537]
hint = 12578819356802034679792891975754306960297043516674290901441811200649679289740456805726985390445432800908006773857670255951581884098015799603908242531673390
q=n//hint
for i in range(99999):
    q+=1
    if n%q==0:
        print(q)
        break
p=n//q
d=inverse(e, (p-1)*(q-1))
print(long_to_bytes(pow(c, d, n)))
print(p)
print((hint-10086)^e)

flag{yihuo_yuan_lai_xian_ji_suan_liang_bian_de2333}

Since you konw something

爆破key即可

1
2
3
4
5
6
7
c=long_to_bytes(218950457292639210021937048771508243745941011391746420225459726647571)

for i in range(2**32):
    key=long_to_bytes(i)
    flag=xor(c,key)
    if flag[:2]==b'fl':
        print(flag)

flag{Y0u_kn0w_th3_X0r_b3tt3r}

茶里茶气

tea加密，解密即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
l  = 199
p  = 446302455051275584229157195942211
v0 = 190997821330413928409069858571234
v1 = 137340509740671759939138452113480
derta = 462861781278454071588539315363
v3 = 489552116384728571199414424951
v4 = 469728069391226765421086670817
v5 = 564098252372959621721124077407
v6 = 335640247620454039831329381071

def decrypt(v0, v1, derta, p, iterations=32):
    v2 = derta*32
    for i in range(iterations):
        v2 = (v2 - derta) % p
        v0 = (v0 - ((v1 + v2) ^ (8 * v1 + v5) ^ ((v1 >> 7) + v6))) % p
        v1 = (v1 - ((v0 + v2) ^ (8 * v0 + v3) ^ ((v0 >> 7) + v4))) % p
    return v0, v1
   

v0, v1=decrypt(v0,v1,derta,p,32)
a=hex((v0<<(l//2))+v1)[2:]
m=''.join(chr(int(a[i:i+2],16)) for i in range(0,len(a),2))
print(m)

flag{f14gg9_te2_1i_7ea_7}

Just one and more than two

多素数和单素数rsa解密即可

1
2
3
4
5
6
7
8
9
10
e = 65537
p=11867061353246233251584761575576071264056514705066766922825303434965272105673287382545586304271607224747442087588050625742380204503331976589883604074235133
q=11873178589368883675890917699819207736397010385081364225879431054112944129299850257938753554259645705535337054802699202512825107090843889676443867510412393
r=12897499208983423232868869100223973634537663127759671894357936868650239679942565058234189535395732577137079689110541612150759420022709417457551292448732371
c1=8705739659634329013157482960027934795454950884941966136315983526808527784650002967954059125075894300750418062742140200130188545338806355927273170470295451
c2=1004454248332792626131205259568148422136121342421144637194771487691844257449866491626726822289975189661332527496380578001514976911349965774838476334431923162269315555654716024616432373992288127966016197043606785386738961886826177232627159894038652924267065612922880048963182518107479487219900530746076603182269336917003411508524223257315597473638623530380492690984112891827897831400759409394315311767776323920195436460284244090970865474530727893555217020636612445
m1=pow(c1,inverse(e,p-1),p)
print(long_to_bytes(m1).decode(),end='')
d=inverse(e,(p-1)*(q-1)*(r-1))
print(long_to_bytes(pow(c2,d,(p*q*r))).decode())

flag{Y0u_re4lly_kn0w_Euler_4nd_N3xt_Eu1er_is_Y0u!}