Symmetric Ciphers
How AES Works
Keyed Permutations
AES(高级加密标准)像所有优秀的块 cipher(分组密码)一样,执行的是“密钥置换”。这意味着它将每个可能的输入块映射到一个唯一的输出块,而具体使用哪个置换则由密钥决定。
- “块”只是指固定数量的位或字节,这可能代表任何类型的数据。 AES处理一个块并输出另一个块。我们将专门讨论AES的变体,该变体可在128位(16个字节)块和128位密钥(称为AES-128)上工作。
使用相同的密钥,可以进行反向排列,将输出块映射回原始输入块。输入块和输出块之间必须保持一对一的对应关系,否则我们无法依赖密文解密回我们开始的相同明文。
一对一对应的数学术语是bijection(双射)。
crypto{bijection}
Resisting Bruteforce
如果分组密码是安全的,攻击者就无法区分 AES 的输出和随机的比特排列。此外,除了简单地暴力破解每个可能的密钥之外,应该没有更好的方法来撤销排列。 这就是为什么学者们认为,如果他们能够找到一种比暴力破解密钥所需的步骤更少的攻击,那么理论上密码就被“破解”了,即使这种攻击实际上是不可行的。
- 破解 128 位密钥空间有多难?有人估计,如果你将整个比特币挖矿网络的算力用于破解 AES-128 密钥,需要超过宇宙年龄一百倍的时间。
事实证明,有一种针对 AES 的攻击比暴力破解更好,但也只是稍微好一点——它将 AES-128 的安全级别降低到 126.1 位,并且已经超过 8 年没有得到改进。 鉴于 128 位提供的巨大“安全裕度”,以及尽管进行了大量研究但仍缺乏改进,因此它不被认为对 AES 安全构成可信风险。但是,是的,从非常狭隘的意义上来说, 它“破坏”了 AES。最后,虽然量子计算机有潜力通过Shor算法。 完全破解 RSA 等流行的公钥密码系统,但人们认为它们只能将通过Grover 算法的对称密码系统的安全级别降低一半。这就是人们推荐使用 AES-256 的原因之一, 尽管它的性能较差,因为它在量子未来仍然可以提供非常足够的 128 位安全性。
针对 AES 的最佳单密钥攻击的名称是biclique
crypto{biclique}
Structure of AES
为了实现一个没有密钥就无法逆推的密钥排列,AES 在输入上应用了大量的临时混合操作。这与基于优雅的单独数学问题的公钥加密系统如 RSA 形成鲜明对比。AES 远没有那么优雅,但它非常快。
在高级别上,AES-128 以“密钥扩展”开始,然后在起始状态上运行 10 轮。起始状态就是我们想要加密的明文块,表示为一个 4x4 字节的矩阵。在 10 轮的过程中,状态矩阵通过一系列可逆变换反复修改。
- 每个转换步骤都有基于 1940 年代由克劳德·香农确立的安全密码理论性质的明确目的。我们将在接下来的挑战中更详细地探讨这些内容。
以下是 AES 加密阶段的概述:
- KeyExpansion or Key Schedule 密钥扩展或密钥调度
从 128 位密钥中,派生出 11 个独立的 128 位“轮密钥”:每个 AddRoundKey 步骤使用一个。
- Initial key addition 初始密钥添加
AddRoundKey 轮密钥加
矩阵中的每一个字节都与初始轮密钥做XOR运算
- Round 循环加密
此阶段循环 10 次,包括 9 个主轮次和 1 个“最终轮次”
SubBytes 字节替代
状态的每个字节根据查找表(“S-box”)替换为不同的字节。
ShiftRows 行移位
将矩阵中的每个横列进行循环式移位
MixColumns 列混淆
了充分混合矩阵中各个直行的操作。这个步骤使用线性转换来混合每列的四个字节。
AddRoundKey 轮密钥加
矩阵中的每一个字节都与当前轮密钥做XOR运算
包括一个
bytes2matrix函数,用于将我们的初始明文块转换为状态矩阵。编写一个matrix2bytes函数,将该矩阵转换回字节,并将结果明文作为标志提交。
1 | def bytes2matrix(text): |
crypto{inmatrix}
Round Keys
我们将暂时跳过密钥扩展阶段的细节。主要点是它接收我们的 16 字节密钥并生成 11 个 4x4 的矩阵,称为“轮密钥”,这些轮密钥是从我们的初始密钥派生出来的。这些轮密钥使得 AES 能够从我们提供的单个密钥中获得额外的性能。
初始密钥添加阶段,接下来只有一个添加轮密钥步骤。添加轮密钥步骤很简单:它将当前状态与当前轮密钥进行异或运算。
AddRoundKey 也出现在每一轮的最后一步。AddRoundKey 是使 AES 成为“密钥置换”而不是仅仅置换的原因。它是 AES 中唯一将密钥混合到状态的部分,但对于确定发生的置换至关重要。
如您在之前的挑战中看到的,如果知道密钥,XOR 是一个容易逆操作的操作,但如果不知道密钥,就很难撤销。现在想象一下尝试恢复被 11 个不同的密钥 XOR 过的明文,并且在每个 XOR 操作之间通过一系列替换和转置密码进行了大量打乱。这正是 AES 所做的!我们将在接下来的几个挑战中看到这种打乱有多有效。
完成
add_round_key函数,然后使用matrix2bytes函数获取下一个 flag。
1 | state = [ |
crypto{r0undk3y}
Confusion through Substitution
每轮 AES 的第一步是 SubBytes。这涉及到将状态矩阵中的每个字节替换为预设的 16x16 查找表中的不同字节。这个查找表被称为“替换盒”或简称“S-box”,一开始可能会让人感到困惑。让我们来分解一下。
1945 年,美国数学家克劳德·香农发表了一篇关于信息论的突破性论文。它将“混淆”确定为安全密码的一个基本属性。“混淆”意味着密文与密钥之间的关系应该尽可能复杂。仅凭密文,不应有任何方法可以了解密钥。
如果一个密文混淆性差,可以将密文、密钥和明文之间的关系表示为线性函数。例如,在凯撒密码中,
ciphertext = plaintext + key。这是一个明显的关联,很容易被逆转。更复杂的线性变换可以使用高斯消元法等技术来解决。即使是低次多项式,例如像x^4 + 51x^3 + x这样的方程,也可以通过代数方法有效地解决。然而,多项式的次数越高,通常解决它就越困难——它只能通过越来越多的线性函数来近似。 S-box 的主要目的是以线性函数难以逼近的方式变换输入。S-box 追求高非线性,尽管 AES 中的 S-box 并不完美,但相当接近。S-box 中的快速查找是执行非常非线性函数的捷径,该函数涉及在伽罗瓦域 2**8 中取模逆,然后应用经过调整以实现最大混乱的仿射变换。表达该函数的最简单方式是通过以下高次多项式:
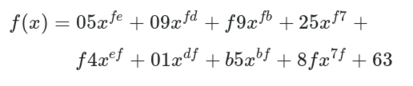
为了制作 S 盒,该函数已对所有从 0x00 到 0xff 的输入值进行了计算,并将输出放入查找表中。
实现
sub_bytes,将状态矩阵通过逆 S 盒发送,然后转换为字节以获取标志。
1 | s_box = (...) |
crypto{l1n34rly}
Diffusion through Permutation
我们已经看到 S-box 替换如何提供混淆。香农描述的另一个关键属性是“扩散”。这关系到加密输入的每一部分应该如何扩散到输出的每一部分。
替换本身会产生非线性,但它不会在整个状态上分布。没有扩散,相同位置的字节在每一轮都会应用相同的变换。这将允许密码分析师分别攻击状态矩阵中的每个字节位置。我们需要通过打乱状态(以可逆的方式)交替替换,以便应用于一个字节的替换会影响状态中的所有其他字节。然后每个输入到下一个 S 盒都成为多个字节的函数,这意味着随着每一轮的进行,系统的代数复杂性会极大地增加。
- 一个理想的扩散量会导致明文中的一个比特变化导致密文统计上有一半的比特发生变化。这种理想的结果被称为雪崩效应。
位移行和混合列步骤结合实现这一点。它们共同工作以确保每个字节在仅两轮内影响状态中的每个其他字节。
ShiftRows 是 AES 中最简单的变换。它保持状态矩阵的第一行不变。第二行向左移动一列,循环。第三行移动两列,第四行移动三列。维基百科表述得很好:“这一步的重要性在于避免列被独立加密,否则 AES 会退化成四个独立的块加密。”
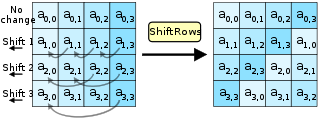
- 图表(以及 AES 规范)显示了
ShiftRows操作以列主序表示。然而,下面的示例代码使用行主序表示状态矩阵,因为在 Python 中这更为自然。只要每次访问矩阵时都使用相同的表示法,最终结果就相同。由于访问模式和缓存行为,使用一种类型的表示法可能会导致更好的性能。
MixColumns 较为复杂。它在 Rijndael 的伽罗瓦域中对状态矩阵的列和预设矩阵进行矩阵乘法。因此,每一列的每个单字节都影响结果列的所有字节。实现细节较为复杂;本页和维基百科都很好地涵盖了它们。
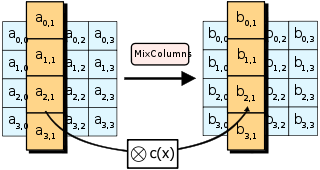
我们提供了执行 MixColumns 和前向 ShiftRows 操作的代码。在实现
inv_shift_rows后,取状态,对其运行inv_mix_columns,然后运行inv_shift_rows,转换为字节,你将得到你的标志。
1 | def shift_rows(s): |
crypto{d1ffUs3R}
Bringing It All Together
除了密钥扩展阶段,我们已经绘制了 AES 的所有组件。我们展示了 SubBytes 如何提供混淆,ShiftRows 和 MixColumns 如何提供扩散,以及这两个属性如何共同工作,在状态上反复循环非线性变换。最后,AddRoundKey 将密钥种入这个替换-置换网络,使加密成为带密钥的置换。
解密涉及逆向执行“AES 结构”挑战中描述的步骤,应用逆操作。请注意,仍然需要先运行 KeyExpansion,并且轮密钥将按逆序使用。AddRoundKey 及其逆操作是相同的,因为 XOR 具有自逆性质。
我们已提供关键扩展代码,以及经过 AES-128 正确加密的密文。复制您迄今为止编写的所有构建块,并完成实现图中步骤的
decrypt函数。解密后的明文是标志。 是的,你可以在这项挑战中作弊,但那样有什么乐趣呢?
这些练习中使用的代码来自 Bo Zhu 的超级简单的 Python AES 实现,因此我们在此处重现了许可证。
1 | N_ROUNDS = 10 |
crypto{MYAES128}
Symmetric Cryptography
Modes of Operation Starter
之前的挑战集展示了 AES 如何在数据块上执行密钥置换。在实践中,我们需要加密比单个数据块更长的消息。操作模式描述了如何在更长的消息上使用像 AES 这样的加密算法。
所有模式在使用不当时都存在严重缺陷。此类挑战将您带到网站的另一部分,您可以在此处与 API 交互并利用这些缺陷。熟悉界面并使用它来获取您的下一个旗帜!
1 | from Crypto.Cipher import AES |
crypto{bl0ck_c1ph3r5_4r3_f457_!}
Passwords as Keys
对称密钥算法中的密钥必须是随机字节,而不是密码或其他可预测数据。随机字节应使用加密安全伪随机数生成器 (CSPRNG) 生成。如果密钥以任何方式可预测,则密码的安全级别会降低,并且攻击者可能会在获得密文访问权限后对其进行解密。
密钥看起来像是由随机字节组成的,并不意味着它一定是。在这种情况下,密钥是使用哈希函数从简单密码中派生出来的,这使得密文可破解。
对于此挑战,您可以编写对端点的 HTTP 请求脚本,或者离线攻击密文。祝你好运!
拿到字典爆破即可,请求太慢了,自己写一下aes解密即可
1 | from Crypto.Cipher import AES |
crypto{k3y5__r__n07__p455w0rdz?}
Block Ciphers 1
ECB CBC WTF
这里您可以使用 CBC 加密,但只能使用 ECB 解密。这不应该是一个弱点,因为它们是不同的模式…对吧?
1 | from Crypto.Cipher import AES |

cbc模式加密,ecb解密,得到dec如下图
1 | from Crypto.Cipher import AES |
crypto{3cb_5uck5_4v01d_17_!!!!!}
ECB Oracle
ECB 是最简单的模式,每个明文块完全独立加密。在这种情况下,您的输入被添加到秘密标志之前并加密,就这么多。我们甚至不提供解密函数。也许当您有“ECB oracle”时,您不需要填充预言机?
1 | from Crypto.Cipher import AES |
先填充一段看看flag长度,发现填充7位的时候,enc长度增加,可知flag长32-6=24位,然后利用填充逐字节爆破即可
1 | from Crypto.Cipher import AES |
crypto{p3n6u1n5_h473_3cb}
Flipping Cookie
您可以为我的网站获取一个 cookie,但这不会帮助您读取标志…我想。
1 | from Crypto.Cipher import AES |
CBC字节翻转,控制iv即可
1 | from Crypto.Cipher import AES |
crypto{4u7h3n71c4710n_15_3553n714l}
Lazy CBC
我只是个懒惰的程序员,想让我的 CBC 加密工作。这些关于初始化向量的讨论是什么意思?听起来并不重要。
1 | from Crypto.Cipher import AES |
题目使用iv作key,根据CBC模式,进行如下加解密
1 | from Crypto.Cipher import AES |
crypto{50m3_p30pl3_d0n7_7h1nk_IV_15_1mp0r74n7_?}
Triple DES
数据加密标准是 AES 的前身,目前在一些发展缓慢的领域如支付卡行业仍被广泛使用。这个挑战展示了 DES 的一个奇怪的弱点,一个安全的分组密码不应该有的。
1 | from Crypto.Cipher import DES3 |
des弱密钥,题目使用的三重des使用两个密钥,使用key1加密,key2解密key1再次加密。加密两次即可获得flag
在 DES 的计算中,56bit 的密钥最终会被处理为 16 个轮密钥,每一个轮密钥用于 16 轮计算中的一轮,DES 弱密钥会使这 16 个轮密钥完全一致,所以称为弱密钥。
有四个弱密钥是绝对不能使用的:
2
3
4
\xFE\xFE\xFE\xFE\xFE\xFE\xFE\xFE
\xE0\xE0\xE0\xE0\xF1\xF1\xF1\xF1
\x1F\x1F\x1F\x1F\x0E\x0E\x0E\x0E如果不考虑校验位的密钥,下面几个也是属于弱密钥的:
2
3
4
\xFF\xFF\xFF\xFF\xFF\xFF\xFF\xFF
\xE1\xE1\xE1\xE1\xF0\xF0\xF0\xF0
\x1E\x1E\x1E\x1E\x0F\x0F\x0F\x0F
1 | from Crypto.Cipher import AES |
crypto{n0t_4ll_k3ys_4r3_g00d_k3ys}
Stream Ciphers
Symmetry
某些分组密码模式,如 OFB、CTR 或 CFB,将分组密码转换为流密码。流密码背后的思想是生成一个伪随机密钥流,然后将其与明文进行异或运算。流密码的一个优点是它们可以处理任意长度的明文,无需填充。
OFB 是一种不为人知的密码模式,在当今使用 CTR 模式时没有实际优势。这个挑战引入了 OFB 的一个不寻常特性。
1 | from Crypto.Cipher import AES |

根据加密流程可以看出,相同的iv和key会生成相同的异或密钥,已知iv加密两次即可得到密文
1 | from Crypto.Cipher import AES |
crypto{0fb_15_5ymm37r1c4l_!!!11!}
Bean Counter
我努力让 PyCrypto 的计数模式做我想做的事情,所以我将 ECB 模式自己转换成了 CTR。我的计数器可以向上和向下移动,以迷惑密码分析师!他们根本不可能阅读我的图片。
1 | from Crypto.Cipher import AES |

仔细看会发现StepUpCounter的实现有问题,会导致if判断一直进else加false导致value不变,png头是已知的,解出密钥异或全部密文即可
1 | from Crypto.Cipher import AES |
crypto{hex_bytes_beans}
CTRIME
我们明文可能存在大量冗余,为什么不先压缩一下呢?
1 | from Crypto.Cipher import AES |
CRIME(英语:Compression Ratio Info-leak Made Easy,意思为:压缩率使信息容易泄露)CVE-2012-4929
zlib会将两段相邻相同的字节压缩,所以可以根据密文长度逐字节进行爆破,只填充一次会爆破不出E,多填几次即可
1 | from Crypto.Cipher import AES |
crypto{CRIME_571ll_p4y5}
Logon Zero
Logon Zero在使用网络之前,您必须使用我们陈旧的 CFB-8 登录协议通过 Active Directory 进行身份验证。
1 | #!/usr/bin/env python3 |
一个登录系统可以选择修改密码,重置密码,使用密码登录获得flag
观察修改密码的过程,将iv逐位加密后异或c,iv长度不够则后补c,意味着我们输入iv的前一部分和c相等时,密码将是重复的相同字节,爆破即可。
1 | from Crypto.Util.number import * |
{‘msg’: ‘Welcome admin, flag: crypto{Zerologon_Windows_CVE-2020-1472}’}
Stream of Consciousness
与我交谈,并从我的加密意识流中听到一句话。
1 | from Crypto.Cipher import AES |