MT19937算法及攻击方式

梅森旋转算法（Mersenne twister）是一种周期很长的的伪随机数生成算法，可以快速的产生高质量的伪随机数，python，php以及多种语言中的随机数模块均采用此算法。

MT19937算法原理

梅森旋转算法的最长周期取自一个梅森素数 219937-1，由此命名为MT9937。常见的两种为32位的MT19937-32和64位的MT19937-64

mt19937的随机数生成器结构由一个32位的种子，然后生成一个具有624个32位数的状态数组。这些整数按顺序输出，全部输出后对该状态应用算法以获取下一组 624 个整数。

生成时分三个过程：

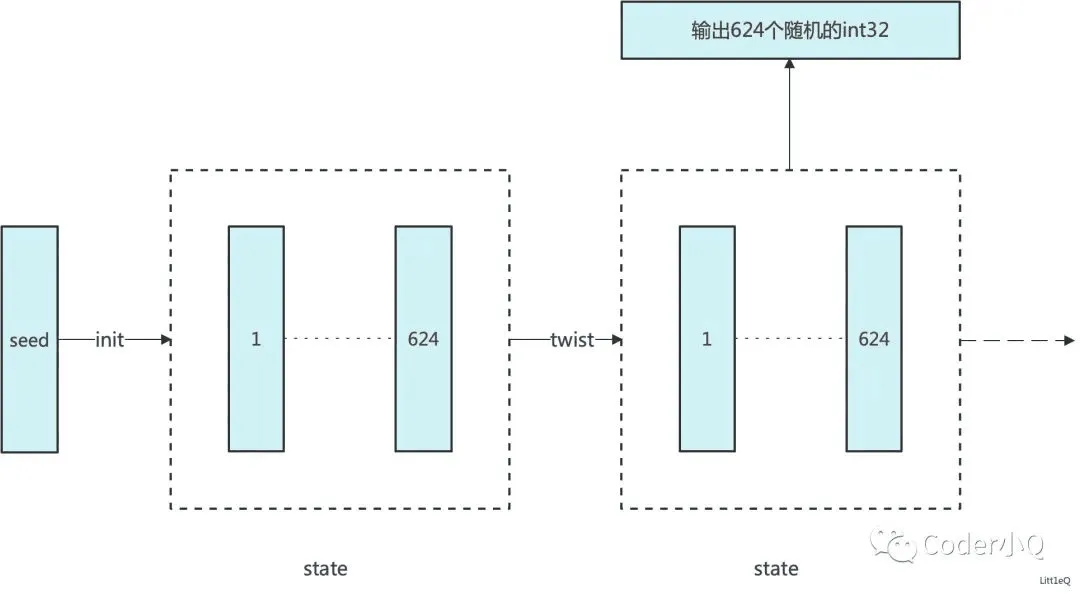
  • 利用seed初始化状态

  • 对状态进行旋转

  • 根据状态提取伪随机数

  • 32位的MT19937的python代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def _int32(x):
    return int(0xFFFFFFFF & x)

class MT19937:
    def __init__(self, seed):
        self.mt = [0] * 624
        self.mt[0] = seed
        self.mti = 0
        for i in range(1, 624):
            self.mt[i] = _int32(1812433253 * (self.mt[i - 1] ^ self.mt[i - 1] >> 30) + i)

	def extract_number(self):
        if self.mti == 0:
            self.twist()
        y = self.mt[self.mti]
        y = y ^ y >> 11
        y = y ^ y << 7 & 2636928640
        y = y ^ y << 15 & 4022730752
        y = y ^ y >> 18
        self.mti = (self.mti + 1) % 624
        return _int32(y)
    
	def twist(self):
        for i in range(0, 624):
            y = _int32((self.mt[i] & 0x80000000) + (self.mt[(i + 1) % 624] & 0x7fffffff))
            self.mt[i] = (y >> 1) ^ self.mt[(i + 397) % 624]
            if y % 2 != 0:
                self.mt[i] = self.mt[i] ^ 0x9908b0df

攻击

已知624组

这种情况只需要将已知的624组填入状态矩阵，即可进行预测和回溯。

有许多可以进行这类攻击的py库，如randcrack，mt19937predictor等，使用方法大同小异。

1
2
3
4
5
6
7
8
9
10
11
from randcrack import RandCrack

#已知连续随机数
data=[...]

RC = RandCrack()
for i in data:
    RC.submit(i)
    
#给出足够多的随机数后，使用predict_getrandbits()即可预测随机数
flag = RC.predict_getrandbits(32)

实际应用中，并不是所有的伪随机数都是32位的，也会出现8位、16位、64位、96位。当然也有可能出现其他不规则的情况。因此，上面提到的“连续624组32位”可以被替换成，“连续19968个比特位”。

任意19968个bit

在使用getrandbits()时如果是输出32的倍数时，会将前生成的32比特放在低位，新生成的拼接在高位。

而getrandbits(16) 中，只返回高16比特，其余比特位被丢弃。getrandbits(33) 中，低 32 比特取自第一组，而高1位取自第二组的最高位比特，第二组低31比特被丢弃。

如果给出了不连续的19968比特，这时候我们可以使用已知的部分构建矩阵求解：

对于每一个比特位bi，可以和状态矩阵state用一个线性关系表示出来 当我们有足够多的b之后就可以构成下面的矩阵方程 其中s和b为长19968的向量，T为19968*19968的矩阵。

如果T是满秩的，求解这个矩阵方程就可以得到s的唯一解，成功复原state，便可以进行溯源和预测。

所以接下来我们只要想办法获得b和T即可。

b的获取

事实上只要我们的已知的任意位置数据大于19968比特即可，但是我们需要知道其对应的位置来确定线性关系以构造方程。

T的获取

虽然已知数据中我们并没有办法获得T，但是其实这个线性关系是可以根据MT19937算法本身得到的。也就是说，如果已知b的对应比特在MT19937产生的随机数输出的位置，则其对应的T也是固定的。

寻找T的过程类似于一个黑盒调用。具体来说，如果我们取s为：(1,0,0,…,0)

按照这个s设置state，然后调用getrandbits(),生成我们已知位置的比特，得到 b’ ，此时得到的 b’ 既是T的第一行。

同理，我们接下来取s：(0,1,0,…,0)

得到T的第二行。全部进行完即可得到完整的T

代码实现：

转载自Explore MT19937 - huangx607087’s Blog

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
Dall=list(map(int,open('data3.txt','r').readlines()))
from Crypto.Util.number import *
from random import *
from tqdm import *
n=1250
D=Dall[:n]
rng=Random()
def getRows(rng):
    #这一部分根据题目实际编写，必须和题目实际比特获取顺序和方式完全一致，且确保比特数大于19937，并且请注意zfill。
    row=[]
    for i in range(n):
        row+=list(map(int, (bin(rng.getrandbits(16))[2:].zfill(16))))
    return row
M=[]
for i in tqdm_notebook(range(19968)):#这一部分为固定套路，具体原因已经写在注释中了
    """
    referennce:
    糖醋小鸡块 2025/1/21 20:26:51
    这部分代码相当于取了一组线性基

    糖醋小鸡块 2025/1/21 20:26:56
    因为mt19937是线性的
    """
    state = [0]*624
    temp = "0"*i + "1"*1 + "0"*(19968-1-i)
    for j in range(624):
        state[j] = int(temp[32*j:32*j+32],2)
    rng.setstate((3,tuple(state+[624]),None)) #这个setstate也是固定格式，已于2025.1.21测试
    M.append(getRows(rng))
M=Matrix(GF(2),M)
y=[]
for i in range(n):
    y+=list(map(int, (bin(D[i])[2:].zfill(16))))
y=vector(GF(2),y)
s=M.solve_left(y)
#print(s)
G=[]
for i in range(624):
    C=0
    for j in range(32):
        C<<=1
        C|=int(s[32*i+j])
    G.append(C)
import random
RNG1 = random.Random()
for i in range(624):
    G[i]=int(G[i])
RNG1.setstate((int(3),tuple(G+[int(624)]),None))

print([RNG1.getrandbits(16) for _ in range(75)])
print(D[:75])